Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 14) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho hình chóp tứ giác đều S.ABCD có chiều cao h, góc ở đỉnh của mặt bên bằng 60°
Câu 11: Cho hình chóp tứ giác đều S.ABCD có chiều cao h, góc ở đỉnh của mặt bên bằng 60°. Tính thể tích hình chóp ?
Lời giải:
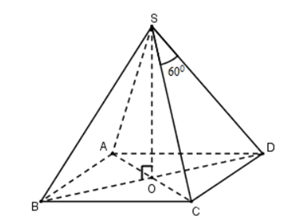
Gọi O = AC ∩ BD
Vì chóp S.ABCD đều nên SO ⊥ (ABCD)
Đặt SA = SB = SC = SD = a
∆SCD có: SC = SD; ^CSD=60° đều ⇒ CD = SC = SD = a
⇒ Hình vuông cạnh ABCD cạnh a ⇒ AC = BD =
SO ⊥ (ABCD) ⇒ SO ⊥ OC ⇒ ∆SOC vuông tại O
Vậy .
Xem thêm các bài giải Tổng hợp kiến thức môn Toán hay, chi tiết khác:
Câu 2: Cho biểu thức. Tìm giá trị của x để P < 1.
Câu 3: Tìm x biết: x + 12 = – 5 – x.
Câu 5: Cho hàm số có đồ thị (C). Hãy chọn mệnh đề sai
Câu 6: Cho α là góc tù và sinα – cosα = . Giá trị của M = sinα – 2cosα là ?
Câu 10: Tính thể tích V của khối chóp tam giác đều S.ABC, biết chiều cao hình chóp bằng h, .
Câu 12: Giả sử x và y là các biến số. Hãy cho biết kết quả của việc thực hiện thuật toán sau
Câu 13: Viết chương trình nhập số nguyên dương n. Kiểm tra n có phải là số nguyên tố hay không ?
Bài viết cùng bài học:




