Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 1) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho tam giác cân tại A, AM là đường cao
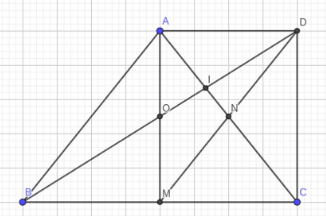
Bài 12: Cho cân tại A, AM là đường cao. Gọi N là trung điểm của AC. D là điểm đối xứng của M qua N.
a) CMR : tứ giác ADCM là hình chữ nhật
b) CMR : tứ giác ABMD là hình bình hành và BD đi qua trung điểm O của AM
c) BD cắt AC tại I. CMR :
Lời giải:
a. Ta có: N là trung điểm AC
M,D đối xứng qua N→ N là trung điểm MD
là trung điểm mỗi đường
Vì
là hình chữ nhật
b. Vì cân tại là trung điểm
AMCD là hình chữ nhật ⇒ AD // CM, AD = CM
⇒ AD // BM, AD = BM
⇒ ABMD là hình bình hành
tại trung điểm mỗi đường
Gọi
⇒ O là trung điểm AM, BD
⇒ BD đi qua trung điểm O của AM
c) Vì O, N là trung điểm AM,DM và
⇒ I là trọng tâm
Vì O là trung điểm BD → OB = OD
Xem thêm các bài giải Tổng hợp kiến thức môn Toán hay, chi tiết khác:
Bài 1. Cho tam giác ABC, M, N, P được xác định bởi véctơ
Bài 2. Cho a,b ≠ -2 thỏa mãn (2a + 1)(2b + 1) = 9
Bài 3. Chứng minh các bất đẳng thức: với a > 0, b > 0
Bài 4. Cho a > 0 và b > 0. Chứng minh rằng
Bài 10. Tính giá trị của biểu thức
Bài 11. Cho a, b, c khác nhau đôi một
Bài 12: Cho cân tại A, AM là đường cao. Gọi N là trung điểm của AC. D là điểm đối xứng của M qua N.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
