Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 47) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho hình bình hành ABCD. Gọi O là giao điểm của 2 đường chéo M, N
Câu 7: Cho hình bình hành ABCD. Gọi O là giao điểm của 2 đường chéo M, N là trung điểm của OD và OB. Gọi E là giao điểm của AM và CD. F là giao điểm của CN và AB.
a, Chứng minh: Tứ giác AMCN là hình bình hành
b, Tứ giác AECF là hình gì?
c, Chứng minh: E, F đối xứng qua O
d, Chứng minh: EC = 2DE.
Lời giải:
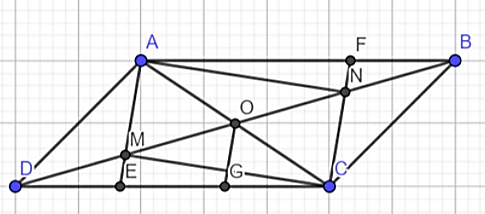
a,
Ta có ABCD là hình bình hành ⇒ AC ∩ BD tại trung điểm mỗi đường
Mà AC ∩ BD = 0 ⇒ O là trung điểm AC, DB
Lại có M, N là trung điểm OD, OB
⇒ OM = OD = OB = ON
⇒ O là trung điểm MN
Do O là trung điểm AC, MN
⇒ AMCN là hình bình hành (đpcm).
b,
Ta có AMCN là hình bình hành.
⇒ AM // CN
⇒ AE // CF
Mà AB // CD ⇒ AF // CE
⇒ AECF là hình bình hành.
c,
Ta có AECF là hình bình hành.
⇒ AC ∩ EF tại trung điểm mỗi đường
Mà O là trung điểm AC
⇒ O là trung điểm EF
⇒ E, F đối xứng nhau qua O (đpcm).
d,
Gọi G là trung điểm CE
Vì O là trung điểm AC ⇒ OG là đường trung bình ∆ACE
⇒ OG // AE
⇒ ME // OG
Mà M là trung điểm DO ⇒ ME là đường trung bình ∆ODG
⇒ E là trung điểm DG
⇒ DE = EG = GC
⇒ CE = CG + GE = DE + DE = 2DE (đpcm).
Xem thêm các bài giải Tổng hợp kiến thức môn Toán hay, chi tiết khác:
Câu 1: Tích 5 × 10 × 15 × 20 × 25 × 30 × ... × 100 có tận cùng bao nhiêu chữ số 0?
Câu 2: Tính tổng các số tự nhiên nhỏ hơn 6
Câu 3: Tính nhanh: 1.4 + 2.5 + 3.6 + ... + 100.103.
Câu 5: 16h40p là bao nhiêu giờ?
Câu 11: Cho tam giác ABC có sin2 C = sin2 A + sin2 B. Tam giác ABC là tam giác gì? Vì sao?
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.