Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 65) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH
Câu 9: Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.
Lời giải:
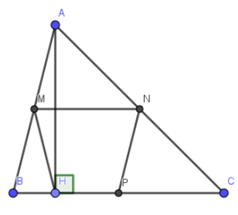
Xét tam giác ABC có M, N lần lượt là trung điểm của AB, AC.
Suy ra MN là đường trung bình.
Do đó MN // BC, hay MN // PH.
Suy ra tứ giác MNPH là hình thang
Xét tam giác ABH vuông tại H có HM là trung tuyến
Suy ra (1)
Xét tam giác ABC có P, N lần lượt là trung điểm của CB, AC
Suy ra PN là đường trung bình
Do đó (2)
Từ (1) và (2) suy ra HM = PN
Xét hình thang MNPH có PN = HM (chứng minh trên)
Suy ra MNPH là hình thang cân (dấu hiệu)
Vậy tứ giác MNPH là hình thang cân.
Xem thêm các bài giải Tổng hợp kiến thức môn Toán hay, chi tiết khác:
Câu 1: Chứng minh nếu p và 8p2 + 1 là hai số nguyên tố lẻ thì 8p2 + 2p + 1 là số nguyên tố.
Câu 3: Phát biểu định lí về hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba.
Câu 4: Cho đường thẳng d: y = 2x + 6. Giao điểm của d với trục tung là
Câu 7: Tổng của tất cả các số nguyên a mà –7 < a ≤ 7 là:
Câu 8: Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?
Câu 11: Phân tích đa thức thành nhân tử: x3 – 7x – 6.
Câu 12: Cho A = [m; m + 1] và B = (–1; 3). Điều kiện để (A ∩ B) = ∅ là gì?
Câu 14: Tìm x, y, z thỏa mãn: x2 + y2 + 2z2 + xy + 2yz + 2zx + x + y + 1 = 0.
Câu 16: Chứng minh rằng 7 . 52n + 12 . 6n chia hết cho 19.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.