Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 2) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy M: 2MC < AC và M không trùng với C
Bài 3: Cho tam giác ABC vuông tại A. Trên cạnh AC lấy M: 2MC < AC và M không trùng với C, vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:
a) Tứ giác ABCD nội tiếp.
b) CA là phân giác góc SCB.
Lời giải:
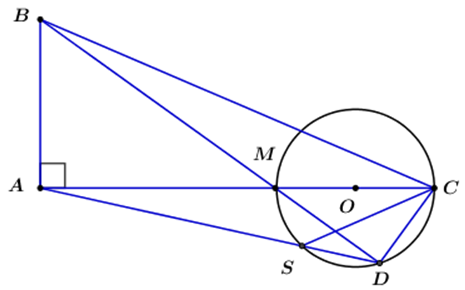
a) Tứ giác ABCD nội tiếp.
Do MC là đường kính của đường tròn (O), D thuộc (O) nên: ∠MDC = 900 = ∠BAC
Suy ra D và A cùng nhìn BC dưới một góc vuông
⇒ Tứ giác ABCD nội tiếp đường tròn đường kính BC.
b) CA là phân giác góc SCB.
Do ABCD là tứ giác nội tiếp nên: ^ADB=^ACB (cùng chắn cung AB).
Xét (O) ta có: ^ACS=^BDA (hai góc nội tiếp cùng chắn cung MS)
⇒ ∠ACB = ∠ ACS ( = ∠BDA).
Vậy CA là phân giác của ∠SCB (đpcm).
Xem thêm các bài giải Tổng hợp kiến thức môn Toán hay, chi tiết khác:
Bài 1: Cho điểm M có hoành độ là -2 và điểm M thuộc đồ thị hàm số y = −2x2 . Xác định tọa độ điểm M
Bài 2: Cho hàm số y = x - 2 có đồ thị là d.Tìm điểm trên d có hoành độ và tung độ đối nhau
Bài 5: Tìm chữ số tận cùng của các số
Bài 8: Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.
Bài 11: Có bao nhiêu số nguyên âm mđể hàm số đồng biến trên khoảng
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.